ChemEng stuff followers

The Hardy-Cross method - An example

 Here a simple two-loop network is analysed to show how to use the Hardy-Cross method. In this example, flow rates, head loss and pressure at nodes are to be calculated using a spreadsheet.

Please, read the posts: The Hardy-Cross method demonstration and The Hardy-Cross method implementation for further reference on the background of this method.

 

CONTENTS

 1 A simple network example

 1.1 The solution procedure

 Step 1 - Flow directions determination

 Step 2 - The mass balance

 Step 3 - The head loss balance

 Step 4 - Flow rate guesses

 Step 5 - The head loss balance equations numerical solution

 Step 6 - Pressure at the nodes

1 A simple network example

Go to the top

Let us consider the following two-loop network (see figure below). For the sake of demonstration, the working fluid shall be taken as water. Also, elevations on each node are taken into account just to show how to use the Hardy-Cross method.

Fig. 01 A simple pipe network. Notice that pipes and nodes are already labeled.


The following data is known,

Table 01 Fluid properties and inlet/outlet flow rates data.


Table 02 Pipe data.


Table 03 Nodes data.

The questions about this network are related to:

  • flow rates on each pipe section,
  • head loss on each pipe section,
  • pressure on each node and
  • hydraulic load $HGL$ on each node.

1.1 The solution procedure

Go to the top

Based on the information provided it seems clear that the first thing that we must do is to set the flow directions in each pipe.

Step 1 - Flow directions determination

Go to the top

The first obvious directions found are those in pipes [1] and [3] going from node A to B and from node A to D, respectively. Since there are outlets in all nodes other than A, it is a little hard to come up with some ideas.

Fig. 02 Flow directions based on inlet at node A.


Looking at the ND of pipes [6] (5 in) and [4] (4 in) it seems reasonable to think part of the fluid coming through [3] would discharge at D and continue through pipe [6]. This is: in [6] the fluid travels from D to E.

Also, pipe [1], having ND=10 in, carries more fluid than [3], with ND=8 in, so that another reasonable idea could be that in pipe [4] the fluid travels from B to E.

Fig. 03 Flow directions based on pipe diameters.


The flow directions through pipes [2] and [7] are determined from common sense. The fluid should travel from B to C and from E to F; otherwise no fluid would exit the network neither at C not at F.

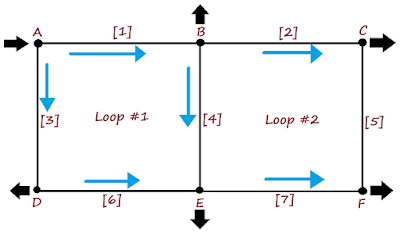Fig. 04 Flow directions based on common sense.


Flow direction through pipe [5] can be determined by thinking about the ND of [2] and [7]. Being [2] the one with the largest ND we can take that the fluid travels from C to F. 

Fig. 05 Flow direction based on pipe's ND.


In Fig. 05, the direction in which the head loss balance is to be done have been introduced already. Notice that for the loops the head loss balance is to be performed in the same direction: clockwise.

Step 2 - The mass balance

Go to the top

Looking at the pipe network in Fig. 05 it is clear that the mass balance is formed of 7 equations: one for the global balance and six at each node. These can easily written as,

$\Sigma Q_{inlet}=\Sigma Q_{outlet}$        Eq. (01) 

which is satisfied if the data in Table 01 is considered. At nodes A, B, C, D, E and F the equations are,

$0.22=Q_1+Q_3$        Eq. (02)

$Q_1=0.06+Q_4$        Eq. (03)

$Q_2=0.04+Q_5$        Eq. (04)

$Q_3=0.04+Q_6$        Eq. (05)

$Q_4+Q_6=0.05+Q_7$        Eq. (06)

$Q_7+Q_5=0.03$        Eq. (07)

You should notice that there are 7 unknowns and only 6 equations so that the flow rates can not be determined from the mass balance.

Step 3 - The head loss balance

Go to the top

The head loss balance can also be written by using the directions set in Fig. 05 and the idea of the Darcy equation for each single pipe section limited by two nodes. In this way, for loop #1 the head loss balance equation is,

$h_L^{(1)}+h_L^{(4)}-h_L^{(6)}-h_L^{(3)}=0$        Eq. (08)

while that for loop #2 is,

$h_L^{(2)}+h_L^{(5)}-h_L^{(7)}-h_L^{(4)}=0$        Eq. (09)

Let us give a little more detail on Eqs. (08-09) by using the Darcy equation definition. This is,

$f_{F1}\dfrac{L_1}{D_1}\dfrac{V_1^2}{2g} + f_{F4}\dfrac{L_4}{D_4}\dfrac{V_4^2}{2g} - f_{F6}\dfrac{L_6}{D_6}\dfrac{V_6^2}{2g} - f_{F3}\dfrac{L_3}{D_3}\dfrac{V_3^2}{2g}=0$        Eq. (10)

and

$f_{F2}\dfrac{L_2}{D_2}\dfrac{V_2^2}{2g} + f_{F5}\dfrac{L_5}{D_5}\dfrac{V_5^2}{2g} - f_{F7}\dfrac{L_7}{D_7}\dfrac{V_7^2}{2g} - f_{F4}\dfrac{L_4}{D_4}\dfrac{V_4^2}{2g}=0$        Eq. (11)

where as you can see all friction factors and flow rates are unknown and as a consequence linear velocities are unkown too. Equations (10-11) already have in it the Hardy-Cross approximation and these are to be used to determined the flow rates. For this purpose, Eqs. (10-11) need to expressed in terms of $Q$'s rather than $V$'s. This is,

$f_{F1}\dfrac{L_1}{D_1}\dfrac{Q_1^2}{2gA_1^2} + f_{F4}\dfrac{L_4}{D_4}\dfrac{Q_4^2}{2gA_4^2} - f_{F6}\dfrac{L_6}{D_6}\dfrac{Q_6^2}{2gA_6^2} - f_{F3}\dfrac{L_3}{D_3}\dfrac{Q_3^2}{2gA_3^2}=0$        Eq. (12)

and

$f_{F2}\dfrac{L_2}{D_2}\dfrac{Q_2^2}{2gA_2^2} + f_{F5}\dfrac{L_5}{D_5}\dfrac{Q_5^2}{2gA_5^2} - f_{F7}\dfrac{L_7}{D_7}\dfrac{Q_7^2}{2gA_7^2} - f_{F4}\dfrac{L_4}{D_4}\dfrac{Q_4^2}{2gA_4^2}=0$        Eq. (13)

Equations (12-13) make use of the Darcy friction factor $f_F$ (not to be confused with the Fanning friction factor).

Please, read the post: Hydraulic equations for non newtonian fluids for more details on the friction factors.

This video can also help you on the friction factors stuff,



Step 4 - Flow rate guesses

Go to the top

Numerical solution to Eqs. (12-13) requires initial guesses for all flow rates. What would be a good set of flow rate guesses? There are some general ideas about this,

  • these guesses should satisfy the mass balance equations,
  • since no flow rate at each pipe section is known you can first guess based on the pipe size,
  • once some flow rate guesses have being set make use the mass balance equations to estimate the other flow rates,
  • repeat if needed.
Now, as you can see the guessed flow rates satisfy the mass balance in the network but these do not satisfy the head loss balance. Remember that the guessed flow rates should satisfy all mass balance equations.
Table 04 Results table with initial guesses for flow rated. Notice that these values satisfy the mass balance equations.


Using the data above you can start the numerical solution.

Step 5 - Head balance equations numerical solution

Go to the top

Now, Eqs. (12-13) are to be solved numerically. For this purpose an iterative approach shall be implemented in a spreadsheet.

Please, read post: The Hardy-Cross method implementation for more details on the spreadsheet preparation.

Let us proceed with Iteration #1 for the loop #1. We shall perform some calculations to estimate head loss $h_L$ on each pipe section of this loop. The table with all calculations looks like this,

Table 05 Calculations for Iteration #1 - Loop #1. Notice that the column (6) for the head losses $h_L$'s and that for the flow rates $Q$'s, column (2),  integrate the sign introduced in the head loss balance (see Eq. (12)). This sign is omitted in the calculations of the velocities in column (3), otherwise imaginary numbers would appear in the column of $f_F$.


From Table 05 a correction to the flow rates (1, 4,6,3) has been obtained in the form of $ \Delta Q=1.42\times 10^{-2}$. Now, Table 04 can be updated as follows,

Table 06 Results updated with the first correction from loop #1. Notice that, all flow rates are taken positive since the sign only makes sense for calculations or while looking to the network (see Fig.  05, for example).


For loop #2 calculations in the iteration #1 the procedure is practically the same. The one thing you must care about is that the corrected flow rates must be used (if any). Once the correction $\Delta Q$ obtained for this loop the involved flow rates must be corrected (including those already corrected). Here is the whole table for Iteration #1,

Table 07 Calculations for Iteration #1 including the two loops in the network. Notice that at loop #2 a second $\Delta Q$ is obtained.


Next, we need to use the $\Delta Q$ correction for flow rates in pipes (2,5,7,4). Flow rate $Q_4$ needs to be corrected again. The results in Table 06 are now updated to be,

Table 08 Results updated with the corrections from loop #2. Notice that the changes in the flow rates are as small as the magnitude of the $\Delta Q$'s.


For the Iteration #2 the same process as above is followed. In this case, the results of Iteration #1 are used as point of start. The results of these calculations are as follows,

Table 09 Calculations for Iteration #2 including the 2 loops. Notice that again, more $\Delta Q$ corrections are obtained.


Table 08 for results is also updated as,

Table 10 Flow rate results from Iteration #2.


The calculations for Iterations #3 and #4 are omitted but the table with the final flow rates are presented below,

Table 11 Results for flow rates for four iterations. In Iteration #4 an average head loss summation of about 0.33 was achieved.


The summations of the head losses per loop indicate how good the balance is. The closer to zero the better the estimation. A good sign of accuracy can be an average $\Sigma h_L<0.01$.

Looking to the change from Iteration #3 to #4 for pipe [1] in Table 11, you can see that the difference is of about 0.2 L/s!. However, it is left to the reader to continue the iteration process until a better accuracy is obtained.

Also, it is left to the reader to check the mass balance Eqs. (02-07) with results of Iteration #4 shown in Table 11. Notice, that the mass balance was only use to give the guessed flow rates at the beginning. Very small departure from the mass balance can be expected. 

Step 6 - Pressure at the nodes

Go to the top

Once the flow rates, with reasonable accuracy has been obtained, pressures and hydraulic loads at each node can be estimated. The procedure to calculate these parameters are based on the equation,


$HGL=\dfrac{p}{\gamma}+z$        Eq. (14)

All you need to do is take the $h_L$'s already calculated in Iteration #4 (or that you may have further calculated). You must care about the signs and the flow direction. The results are given below.

Table 12 Rsults for pressure and hydraulic load at each node in the network.


This is the end of the post. I hope you could find it useful.

Any question? Write in the comments and I shall try to help.

Other stuff of interest

No comments:

Post a Comment

Subscribe to: Posts (Atom)

Most popular posts